Bayesian Outlier Detection

Calculate the posterior probability that the absolute value of error exceeds more than k standard deviations P(|epsilon_j| > k sigma | data) under the model Y = X B + epsilon, with epsilon ~ N(0, sigma^2 I) based on the paper by Chaloner & Brant Biometrika (1988). Either k or the prior probability of there being no outliers must be provided. This only uses the reference prior p(B, sigma) = 1; other priors and model averaging to come.

Usage

Bayes.outlier(lmobj, k, prior.prob)

Arguments

lmobj

An object of class `lm`

k

number of standard deviations used in calculating probability of an individual case being an outlier, P(|error| > k sigma | data)

prior.prob

The prior probability of there being no outliers in the sample of size n

Value

Returns a list of three items:

e

residuals

hat

leverage values

prob.outlier

posterior probabilities of a point being an outlier

prior.prob

prior probability of a point being an outlier

References

Chaloner & Brant (1988) A Bayesian Approach to Outlier Detection and Residual Analysis Biometrika (1988) 75, 651-659

Examples

data("stackloss")
stack.lm <- lm(stack.loss ~ ., data = stackloss)
stack.outliers <- Bayes.outlier(stack.lm, k = 3)
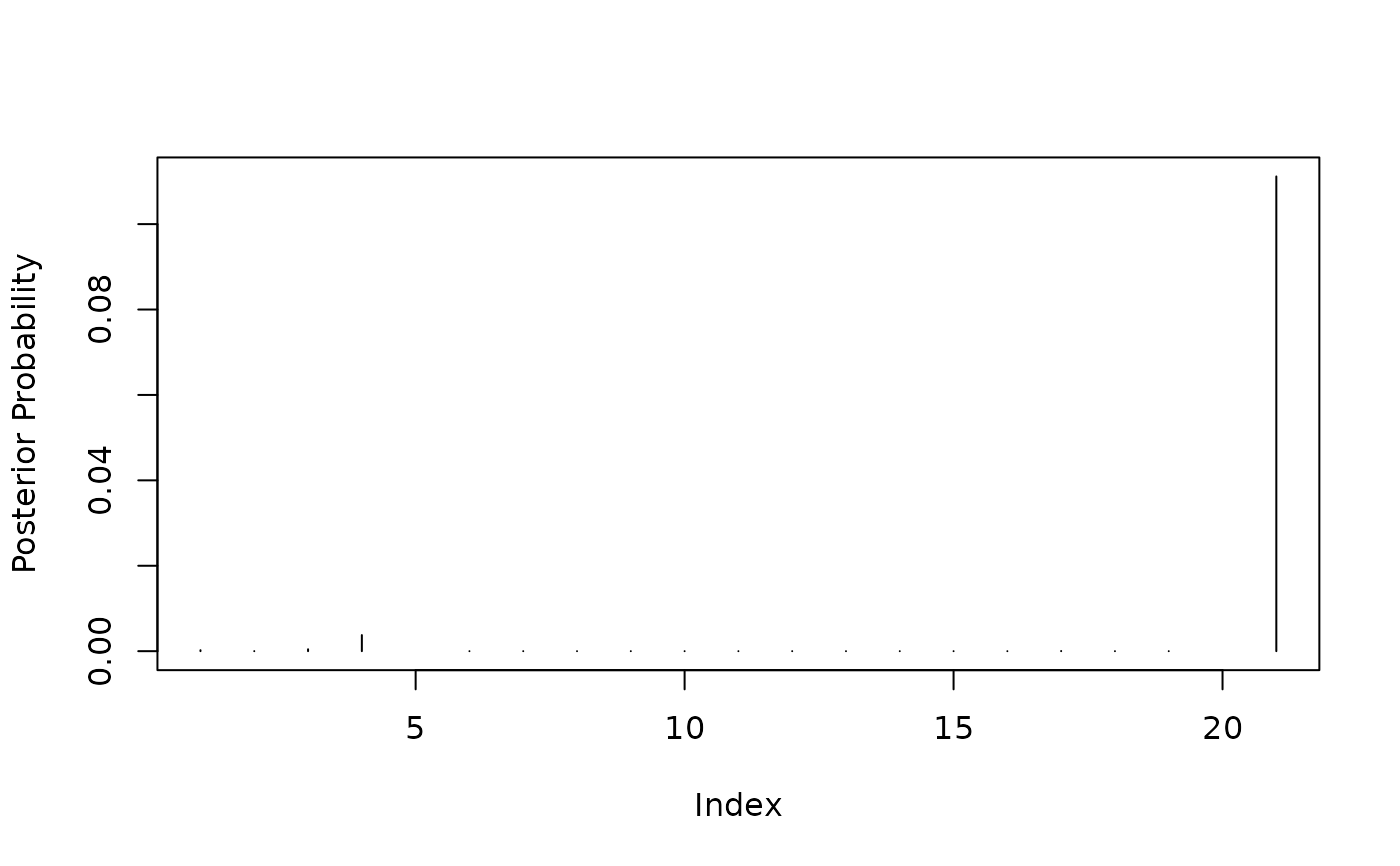
plot(stack.outliers$prob.outlier, type = "h", ylab = "Posterior Probability")

# adjust for sample size for calculating prior prob that a
# a case is an outlier
stack.outliers <- Bayes.outlier(stack.lm, prior.prob = 0.95)
# cases where posterior probability exceeds prior probability
which(stack.outliers$prob.outlier > stack.outliers$prior.prob)
#> [1]  4 21